技术
三角函数是用直角三角形的边的比来定义的,表示的是对应某个角度的边与边之间的比例,在测绘计算中广泛应用。三角函数本是数学定义出来的计算工具,但可以非常好地描述波动等众多的自然现象。这里我们将在中学课本的基础上,进一步介绍三角函数的微积分、三角函数具有的"正交性",以及在天文观测、人工声音等领域常用的工具—傅里叶变换,带你进入更深奥的三角函数的世界。
翻译/陈敏
正弦、余弦、正切的定义
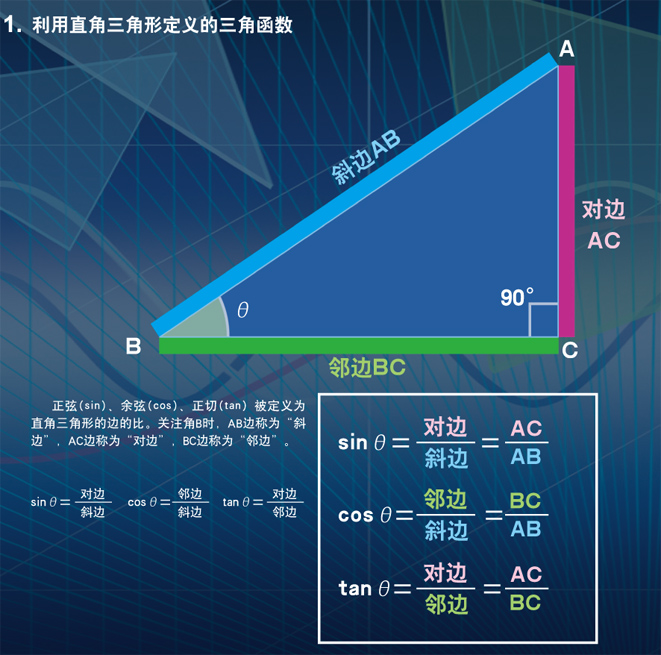
1.利用直角三角形定义的三角函数
正弦(sin)、余弦(cos)、正切(tan)被定义为直角三角型的边的比。关注角B时,AB边称为"斜边", AC边称为"对边",BC边称为"邻边"。
设角B的大小为θ时,它们分别表示为;
对边 邻边 对边
sinθ = ------- cosθ = ------ tanθ = ------
斜边 斜边 邻边
对边 AC
sinθ = ------- = -------
斜边 AB
对边 AC
tanθ = ------ = -------
邻边 BC
2.用半径为1的圆来定义三角函数
用直角三角型的边的比来定义三角函数的话,可描述的角度的值被局限在0°~90°的范围之内。为了消除这个局限,我们用半径为1的圆来重新定义三角函数。也就是说,当点P从点A(1,0)开始在圆周上逆时针转过角度θ时, P点的x坐标的值就是cosθ、P点的y坐标的值就是sinθ。当点P顺时针转动时,其角度为负值(-)。
附件: